I'm reading the book Expert F# by Don Syme et al. In chapter 3 - Introducing Functional Programming, pg. 29 is listed the F# Bitwise Arithmetic Operators. They are shown in Table 1:
| Operator | Description | Sample | Use Result |
|---|---|---|---|
| &&& | Bitwise “and” | 0x65 &&& 0x0F | 0x05 |
| ||| | Bitwise “or” | 0x65 ||| 0x18 | 0x7D |
| ^^^ | Bitwise “exclusive or” | 0x65 ^^^ 0x0F | 0x6A |
| ~~~ | Bitwise negation | ~~~0x65 | 0xFFFFFF9a |
| <<< | Left shift | 0x01 <<< 3 | 0x08 |
| >>> | Right shift (arithmetic if signed) | 0x65 >>> 3 | 0x0C |
The sample given to help with the understanding of such operators is about an integer encoder. Read the sample statement:
The following sample shows how to use these operators to encode (signed) 32-bit integers into 1, 2, or 5 bytes, represented by returning a list of integers. Integers in the range 0 to 127 return a list of length 1.
The proposed solutions is:
let encode (n: int32) = if (n >= 0 && n <= 0x7F) then [ n ] elif (n >= 0x80 && n <= 0x3FFF) then [ (0x80 ||| (n >>> 8)) &&& 0xFF; (n &&& 0xFF) ] else [ 0xC0; ((n >>> 24) &&& 0xFF); ((n >>> 16) &&& 0xFF); ((n >>> 8) &&& 0xFF); (n &&& 0xFF) ]
As I have never spent time with code that handles individual bits I had a tough time to understand what was going on with this code. I didn't go further reading the book until I could understand the problem through and through. Obviously the problem statement is clear. The input and output is clearly stated. No doubt. The problem I had was to understand how the code was producing the output. What did I do? I spent some time reading about the bitwise operations. For sure I've studied it on college but I haven't practiced it programmatically through coding. I did lots of exercises about this matter but only analytically, that is, using sheets of paper. Sometimes it's good to write things down and be the processor for an instant! :-)
I executed the above code mentally and even wrote some test cases to make sure I was understanding the intrinsic aspects of it.
Bellow are the annotations I did to exercise the problem analytically. I provide them so that you can use the annotated calculations to better realize what's going on during the computations:
(* The following sample shows how to use Bitwise Operators to encode (signed) 32-bit integers into 1, 2, or 5 bytes, represented by returning a list of integers. Integers in the range 0 to 127 return a list of length 1: *) let encode (n: int32) = // from n >= 0 && n <= 127 if (n >= 0 && n <= 0x7F) then [ n ] // from n >= 128 && n <= 16383 255 elif (n >= 0x80 && n <= 0x3FFF) then [ (n >>> 8)) &&& 0xFF; (* 192 *) (* 255 *) (n &&& 0xFF) ] else [ 0xC0; ((n >>> 24) &&& 0xFF); ((n >>> 16) &&& 0xFF); ((n >>> 8) &&& 0xFF); (n &&& 0xFF) ] (* Date: 05-08-2008 Hexa | Decimal | Binary 0x7F 127 0x80 128 10000000 0x3FFF 16383 0xFF 255 11111111 0xC0 192 e.g.: n = 7777 falls into the elif statement returning a list of [2 bytes] 1st byte 1111001100001 = 7777 0000000011110 (n >>> 8) ||| 10000000 = 128 -------- 10011110 = 158 &&& 11111111 = 255 -------- 10011110 = 158 2nd byte 1111001100001 = 7777 &&& 0000011111111 = 255 ------------- 0000001100001 = 97 list = [158; 97] e.g.: n = 100000 falls into the else statement returning a list of [5 bytes] 1st byte = 0xC0 = 192 2nd byte 11000011010100000 = 100000 000000000000000000000000 (n >>> 24) &&& 11111111 = 255 ----------------- 00000000000000000 = 0 3rd byte 11000011010100000 = 100000 00000000000000001 (n >>> 16) &&& 11111111 = 255 ----------------- 1 = 1 4th byte 11000011010100000 = 100000 00000000110000110 (n >>> 8) &&& 011111111 = 255 ----------------- 010000110 = 134 5th byte 11000011010100000 = 100000 &&& 00000000011111111 = 255 ----------------- 00000000010100000 = 160 list = [192; 0; 1; 134; 160] Reference: http://en.wikipedia.org/wiki/Bitwise_operation#AND *)
I definitely understood the code while I was writing the above annotations. So, what exactly do the bitwise operators do? Consider for example this fragment of the above F# code:
((n >>> 8) &&& 0xFF);
Suppose that n is equal 9876.
Let's convert n to the binary numeral system:
| Operation | Remainder |
|---|---|
| 9876 ÷ 2 = 4938 | 0 |
| 4938 ÷ 2 = 2469 | 0 |
| 2469 ÷ 2 = 1234 | 1 |
| 1234 ÷ 2 = 617 | 0 |
| 617 ÷ 2 = 308 | 1 |
| 308 ÷ 2 = 154 | 0 |
| 154 ÷ 2 = 77 | 0 |
| 77 ÷ 2 = 38 | 1 |
| 38 ÷ 2 = 19 | 0 |
| 19 ÷ 2 = 9 | 1 |
| 9 ÷ 2 = 4 | 1 |
| 4 ÷ 2 = 2 | 0 |
| 2 ÷ 2 = 1 | 0 |
| 1 ÷ 2 = 0 | 1 |
Reading the sequence of remainders from the bottom up gives the binary number 100110100101002. The subscript 2 is to say that this is a binary number representation (base 2).
Right shift operation
The bitwise operator >>> (right shift) is applied to the bits that represent the integer (decimal) value of n. By right shifting we in fact push zeros toward the right side of the string of bits. The once least significant bits of the representation are then discarded.
The code above will right shift the value 100110100101002 by 8, that is, 8 zeros will be inserted into the start of the string of bits pushing the least significant bits out of it. What we get is:
10011010010100 = 987610
00000000100110 = 3810 = (n >>> 8)
Bitwise "and" operation
The bitwise operator &&& (bitwise “and”) is then applied to the result of the right shifting operation just executed. It does nothing and is used here just for the sake of exemplification. Therefore the next operation that will be performed is:
00000000100110 = 3810
&&& 11111111 = 8 bits = 1 byte = 25510
--------
00100110 = 3810
The comparison process is done in pairs of bits - 1 bit of each string of bits. When the bits that compose the pair are equal 1 the "and" operator outputs 1 otherwise 0.
As you can see the value remains the same after the bitwise "and" operation.
There is a case in which the bitwise "and" operator executes a different operation. The following line of code shows it:
(n &&& 0xFF)
Note that this time there's no right shifting operation. In this case what happens is:
10011010010100 = 987610
&&& 11111111 = 0xFF16 = 25510
--------
10010100 = 14810
The above operation is executed so that it's possible to isolate part of the string of bits. The binary representation is broken in chunks of bytes. 1 byte is equal 8 bits.
According to the problem statement. The integer value n will be encoded into 1, 2 or 5 bytes. To achieve this the right shift operator (>>>) and the bitwise "and" operator (&&&) are used so that each chunk of 8 bits is analyzed and then converted to a byte that'll then be represented by its integer value.
The first byte from left to right of n is 100110. Its second byte is 10010100.
The output list of the code would be: [100110; 10010100] = [38; 148]
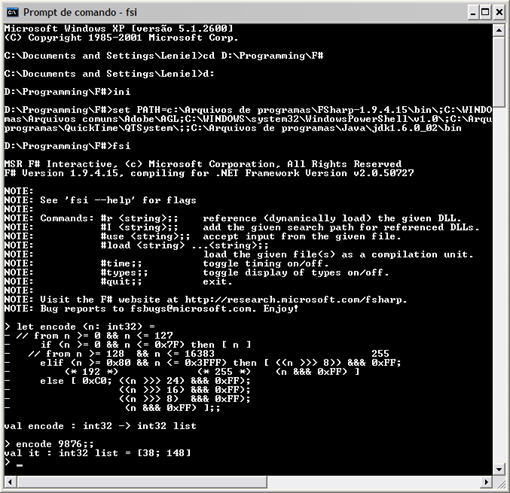
The following is the screenshot of the real program being executed:
As you see the output matches the analytical reasoning exercised in this post.
Left shift bitwise operation
The bitwise operator <<< (left shift) does just the opposite of the right one, that is, instead of pushing zeros toward the right of the string of bits it actually pushes zeros toward the left. This changes the most significant bits.
For example, the sample given on Table 1 is 0x01 <<< 3 that'll will output a result equal to 0x08. 0x0116 = 110 and 0x0816 = 810. You may be asking yourself: what are those 0x at the beginning of each value. It's the form used to represent an hexadecimal (base 16) inside the programming language.
Getting back to the point, let's get the binary representation of 110: it is 12. This way, left shifting by 3 we'll get:
0001 = 110
1000 = 810 = (1 <<< 3)
Bitwise "or" operation
The bitwise "or" operator (|||) is the opposite of the "and" operator.
For example, the sample given on Table 1 is 0x65 ||| 0x18 that'll output 0x7D. 0x65 = 10110 and 0x1816 = 2410. 0x7D16 = 12510 . We have that 10110 = 11001012 and 2410 = 110002 . This way, applying the bitwise "or" operator we get:
1100101 = 10110
||| 0011000 = 2410
-------
1111101 = 12510
Note that additional zeros were added to the second string of bits so that it has the same length of the first.
Again the operation is done by comparing pairs of bits. One of each string of bits at a time. When any of the bits that compose the pair are equal 1 the "or" operator outputs 1. The unique case in which the output is 0 is when both bits are equal 0.
Bitwise “exclusive or” or XOR operation
The bitwise "exclusive or" operator (^^^) outputs 1 if the bits being compared are different or 0 if they are equal.
For example, the sample given on Table 1 is 0x65 ^^^ 0x0F that'll output 0x6A. 0x65 = 10110 and 0x0F16 = 1510. 0x6A16 = 10610 . We have that 10110 = 11001012 and 10610 = 11010102 . This way, applying the “exclusive or” operator we get:
1100101 = 10110
^^^ 0001111 = 1510
-------
1101010 = 10610
Bitwise negation or one's complement operation
The bitwise "negation" operator (~~~) is an unary operator that inverts the value of the bit. The operation is done bit by bit. If the bit is 1 then the operator outputs 0 otherwise if it is 0 then the operator outputs 1. It forms the one's complement of a given number.
For example, the sample given on Table 1 is ~~~0x65 that'll output 0xFFFFFF9a. 0x65 = 10110 and 0xFFFFFF9a16 = -10210. This way, applying the "negation" operator we get:
~~~ 01100101 = 10110
--------
10011010 = -10210
Final notes notes
I hope that you have gotten the principles behind the bitwise arithmetic operators.
Important: do not try to make sense of the encoder code because as the name says it's an encoder, so there are customizations implemented on it, that is, how to dispose the bytes into the output list is done according to the developer's will. That's why it's an encoder. Only who has the encoding pattern can decodes the encoded data! :-)
A good tip: use the computer calculator to exercise more examples. I use the Windows calculator in its scientific fashion/configuration. You can change its standard view through the View menu.