Compilers construction paper
I and a dear brother in faith of mine called Wellington Magalhães Leite wrote a paper titled: Fortran Numerical Constants Recognizer
It exercises concepts related to state transition diagram, finite state machine and automata theory.
Needless to say, compilers construction was one of the best disciplines or even the best discipline I had in the computer engineering course. I really like this kind of stuff. State machines and automata theory really rocks! Automata theory is other discipline I had that really got my attention.
State Transition Diagram
This is the lexical state transition diagram in which our work is based:
Alphabet = {d, +, - , . , E} (d is any digit)
The arches of any vertex to an Error vertex aren’t showed but they exist.
Expressions like the following are recognized: 13, +13, -13, 13., 1.25, .25, -.25, -32.43, 13E-15, 13.E-15, -13.25E+72, .75E5, etc.
Expressions like the following aren’t recognized: ++13, .E13, etc.
The vertex with a 0 (zero) value is the initial state.
The vertexes with bold circles are the final states.
Note: It’s important to note that lexical state transition diagrams are finite automatons.
Abstract
A didactic method for the construction of a compiler front-end is the one substantiated in transition diagrams. So, its construction helps with the familiarization regarding the tasks of a compiler project.
This paper presents a Fortran numerical constants recognizer. It is developed based on a state transition diagram and its implementation follows the standards of the C# programming language.
Keywords: fortran, compiler construction, state transition diagram, C# programming language
CONTENTS
1 INTRODUCTION 6
1.1 Objective 6
1.2 Definition 6
2 DEVELOPMENT 7
2.1 Mapping the constants 7
2.2 Mapping the functions 7
2.3 Application main entry point 10
3 APPLICATION 12
3.1 Validating expressions 12
3.1.1 Single expression 12
3.1.2 Set of expressions 13
4 CONCLUSION 14
5 REFERENCES 15
6 ADDENDUM 16
Resumo
Um método muito didático para a construção do front-end de um compilador é aquele fundamentado em diagramas de transição. Logo, seu estudo ajuda na familiarização com as atividades envolvidas no projeto de um compilador.
Esse trabalho apresenta um sistema reconhecedor de constantes numéricas em Fortran. O mesmo é desenvolvido a partir de um diagrama de transição de estados e sua codificação segue os padrões e moldes da linguagem de programação C#.
Palavras-chave: fortran, construção de compiladores, diagrama de transição de estados, linguagem de programação C#
SUMÁRIO
1 Introdução 5
1.1 Objetivo 5
1.2 Definição 5
2 Desenvolvimento 6
2.1 Mapeamento das constantes 6
2.2 Mapeamento das funções 6
2.3 Mapeamento da chamada principal 10
3 Aplicação 12
3.1 Validação de expressões 12
3.1.1 Uma única expressão 13
3.1.2 Uma lista de expressões 14
4 Conclusão 15
5 Bibliografia 16
6 Anexo 17
Source code
class StateTransitionSystem { public static void Main(string[] args) { Console.Title = "State Transition System for recognizing numeric constants in FORTRAN"; Console.BackgroundColor = ConsoleColor.White; Console.ForegroundColor = ConsoleColor.Black; char ch; do { Console.Clear(); // Print startup banner Console.Write("\nState Transition System C# Sample Application\n"); Console.Write("Copyright ©2006 Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.\n\n"); Console.Write("UBM COMPUTER ENGINEERING - 7TH SEMESTER [http://www.ubm.br/]\n\n"); // Describes program function Console.Write("This program example demonstrates the State Transition Diagram's algorithm for\n"); Console.Write("numeric constants validation in FORTRAN.\n\n"); // Describes program's options Console.Write("You can validate expressions by two different ways as follow:\n\n"); Console.Write("1 - A single expression by providing an entry.\n\n"); Console.Write("2 - A set of expressions by providing an input file.\n"); Console.Write(" * Notice: the expressions must be separeted in-lines.\n"); Console.Write("\n\nEnter your choice: "); ch = Console.ReadKey().KeyChar; switch(ch) { case '1': { SingleExpression(); break; } case '2': { SetOfExpressions(); break; } } } while(ch == '1' || ch == '2'); } /// <summary> /// Enumeration where each item corresponds to one state in the State Transition Diagram. /// </summary> public enum PossibleStates { s0 = 0, s1, s2, s3, s4, s5, s6, s7, error } /// <summary> /// Array of type PossibleStates, which contains the finalStates acceptable by the /// State Transition Diagram. /// </summary> public static PossibleStates[] finalStates = { PossibleStates.s2, PossibleStates.s3, PossibleStates.s6 }; /// <summary> /// Verifies if the last state achieved by the machine belongs to the finalStates /// array. /// </summary> public static bool IsFinalState(PossibleStates currentState) { for(int i = 0; i < finalStates.Length; i++) if(currentState == finalStates[i]) return true; return false; } /// <summary> /// Recognizes the current state and the character “label” being analysed, values /// passed as parameters. After, the function does the transition of state case some /// condition is satisfied, otherwise, the function will return an error flag. /// </summary> public static PossibleStates Recognizer(PossibleStates currentState, char c) { switch(currentState) { case PossibleStates.s0: { if(c == '+' || c == '-') return PossibleStates.s1; if(char.IsDigit(c)) return PossibleStates.s2; if(c == '.') return PossibleStates.s4; break; } case PossibleStates.s1: { if(char.IsDigit(c)) return PossibleStates.s2; if(c == '.') return PossibleStates.s4; break; } case PossibleStates.s2: { if(char.IsDigit(c)) return PossibleStates.s2; if(c == '.') return PossibleStates.s3; if(c == 'E') return PossibleStates.s5; break; } case PossibleStates.s3: { if(char.IsDigit(c)) return PossibleStates.s3; if(c == 'E') return PossibleStates.s5; break; } case PossibleStates.s4: { if(char.IsDigit(c)) return PossibleStates.s3; break; } case PossibleStates.s5: { if(char.IsDigit(c)) return PossibleStates.s6; if(c == '+' || c == '-') return PossibleStates.s7; break; } case PossibleStates.s6: { if(char.IsDigit(c)) return PossibleStates.s6; break; } case PossibleStates.s7: { if(char.IsDigit(c)) return PossibleStates.s6; break; } } return PossibleStates.error; } /// <summary> /// Reads an input expression, recognizes its characters, changes the states /// accordingly to those characters and hence validates the entry. /// </summary> public static void SingleExpression() { do { // The machine points to the initial state of the State Transition Diagram. PossibleStates currentState = PossibleStates.s0; Console.Write("\n\nEnter the expression to be evaluated: "); // strExpression receives the entry typed by the user. string strExpression = Console.ReadLine(); /* For each string's character (label), calls the function Recognizer that on the other hand changes the machine state accordingly. */ for(int i = 0; strExpression.Length > i; ++i) if(currentState != PossibleStates.error) currentState = Recognizer(currentState, strExpression[i]); else break; /* Calls the function IsFinalState to verify if the state where the machine stopped is a final state or not. */ if(IsFinalState(currentState)) Console.WriteLine("\n Valid expression.\n"); else Console.WriteLine("\n Invalid expression!\n"); Console.Write("Do you wanna try again? (y\\n) "); } while(Console.ReadKey().KeyChar == 'y'); } /// <summary> /// Reads an input file, recognizes its lines, expression by expression and changes /// the states accordingly to each expression. In other words, validates the entire /// list. /// </summary> public static void SetOfExpressions() { do { Console.Write("\n\nEnter the file path: "); // Obtains the file name. string fileName = Console.ReadLine(); // Verifies if the file exists. if(!File.Exists(fileName)) Console.Write("\n File not found!\n\n"); else { // Reads all the file's lines and stores them. StreamReader sReader = new StreamReader(fileName); string expression; // Evaluates each line until achieve the EOF (end of file). while((expression = sReader.ReadLine()) != null) { // The machine points to the initial state of the State Transition Diagram. PossibleStates currentState = PossibleStates.s0; /* For each expression's character (label), calls the function Recognizer that on the other hand changes the machine state accordingly. */ for(int i = 0; expression.Length > i; ++i) if(currentState != PossibleStates.error) currentState = Recognizer(currentState, expression[i]); else break; /* Calls the function IsFinalState to verify if the state where the machine stopped for the expression is a final state or not. */ if(IsFinalState(currentState)) Console.WriteLine("\n{0} is a valid expression.", expression); else Console.WriteLine("\n{0} is an invalid expression!", expression); } sReader.Close(); } Console.Write("\nDo you wanna try again? (y\\n) "); } while(Console.ReadKey().KeyChar == 'y'); } }
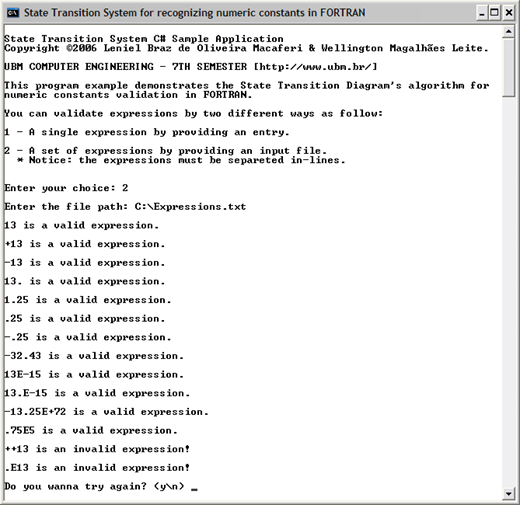
Screenshots
See screenshots of Fortran numerical constants recognizer in action:

You can get a PDF copy of the paper and the accompanying Fortran Numerical Constants Recognizer files in a ZIP file at:
English version
http://leniel.googlepages.com/FortranNumericalConstantsRecognizer.pdf
Portuguese version
http://leniel.googlepages.com/SisReconhecedorConstNumericasFortran.pdf
Microsoft Visual Studio C# 2008 Console Application project
http://leniel.googlepages.com/FortranNumericalConstantsRecognizer.zip
Note: The program’s source code is in a Microsoft Visual Studio C# 2008 Console Application project. If you don’t have Visual Studio, you can get a free copy of its express edition at http://www.microsoft.com/express/download.





