Leniel Maccaferri's blog: Development and Numerical Simulation of ODEs in C

Ordinary Differential Equation
In mathematics, an ordinary differential equation (or ODE) is a relation that contains functions of only one independent variable, and one or more of its derivatives with respect to that variable. To get in depth knowledge about ODEs refer to this article at Wikipedia.

A scientific magazine article
As the result of the Numerical Calculus discipline's classwork during the 4th term of the computer engineering course I and the teacher Dener Martins dos Santos decided to write an article about ordinary differential equations. In that discipline we studied about the classic methods for the resolution of ordinary differential equations.

We ended up with a concise informative article with the following title: Development and Numerical Simulation of Algorithms to Computational Resolution of Ordinary Differential Equations. Then we submitted the article to the scientific magazine of my alma mater university. We made it in the magazine called Revista Científica do Centro Universitário de Barra Mansa.

See the article's abstract below:

The computational simulation nowadays consists of a great tool assisting the learning process of complex mathematical calculations. This informative article shows how the computational resolution of differential equations assists in this learning. Two different types of computational resolution for differential equations are demonstrated: explicit Euler's method and Runge-Kutta's fourth order method. The programs were developed in C programming language. The results obtained via both methods are compared with the respective analytical solution (traditional, manual); in these a low level of generated computational error was perceived during their simulation, not compromising the methods.

Keywords: ordinary differential equations, numerical methods, C programming.

SUMMARY
1 INTRODUCTION
2 OBJECTIVE
3 REVISION
4 METHODOLOGY
  4.1 Programs
5 RESULTS
  5.1 Differential equation 1
      5.1.1 Initial conditions
      5.1.2 Analytical solution (traditional)
      5.1.3 Graphical solution
            5.1.3.1 Explicit Euler’s method
            5.1.3.2 Runge-Kutta’s fourth order method
  5.2 Differential equation 2
      5.2.1 Initial conditions
      5.2.2 Analytical solution (traditional)
      5.2.3 Graphical solution
            5.2.3.1 Explicit Euler’s method
            5.2.3.2 Runge-Kutta’s fourth order method
6 CONCLUSION
7 BIBLIOGRAPHY

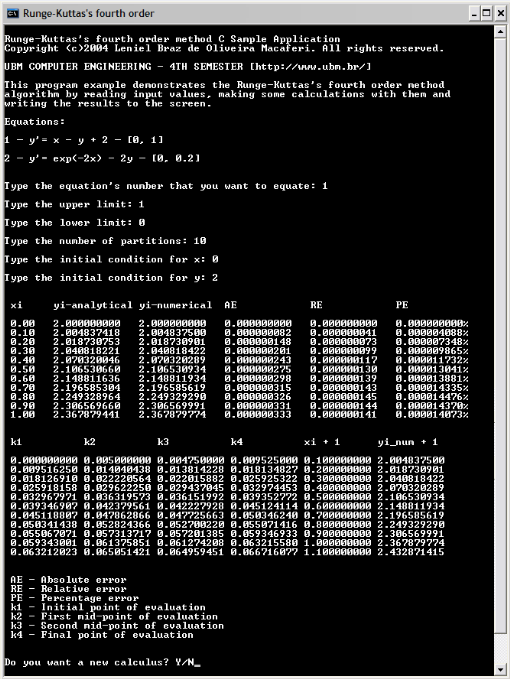
See a screenshot of the output of Runge-Kutta's fourth order method when simulated with the 1st equation described in the paper: